
Photo by Annie Theby on Unsplash
Probabilistic Data Structures: Bloom filter
Understanding one of the most popular probabilistic data structures
If you have a glass-protected bookshelf, it will protect your books from dust and insects. However, it will cost you more time to access the books when you need them, since you first need to slide or open the glass before you can get the books. Then again, if it’s an open bookshelf, it will give you quicker access to the books, but you will lose the layer of protection.
Similarly, if you organize your books in lexicographic order, you can easily search for a book if you know its name. But if your bookshelf has cases of different sizes, you will have to organize your books based on their size. It will look nice, but can you find a book in a hurry? I don’t think so.
Data structures are nothing different. They are like the bookshelves of your application where you can organize your data. Different data structures will give you different facility and benefits. To properly use the power and accessibility of the data structures, you need to know the trade-offs.
Main-stream data structures, like Lists, Maps, Sets, Trees etc. are mostly used for achieving certain results about whether the data exists or not, maybe along with the number of occurrences and such. Probabilistic data structures, however, will give you memory-efficient and faster results — at the cost of providing a probable result instead of a certain one.
Right now, it might not seem intuitive to use such data structures. But, in this piece, I’ll try to convince you that these type of data structures have their specific use cases, and that you might find them useful in certain scenarios.
In this piece, I’ll talk about one of the most popular probabilistic data structures called Bloom filter. In the future, I’ll try to write about some others.
Bloom Filter
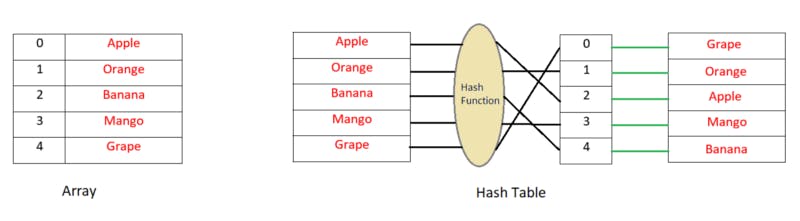
Do you know how hash tables work?
When you insert new data in a simple array or list, the index, where this data would be inserted, is not determined from the value to be inserted. That means there is no direct relationship between the key (index) and the value (data). As a result, if you need to search for a value in the array you have to search in all of the indexes.
Now, in hash tables, you determine the key or index by hashing the value. Then you put this value in that index in the list. That means the key is determined from the value, and every time you need to check if the value exists in the list, you just hash the value and search on that key. It’s pretty fast and will require O(1) searching time in Big-O notation.
Now, let’s consider that you have a huge list of weak passwords and it is stored on some remote server. It’s not possible to load them at once in the memory/RAM because of the size. Each time a user enters his/her password, you want to check if it is one of the weak passwords. If it is, you want to give him/her a warning to change it to something stronger. What can you do?
As you already have the list of the weak passwords, you can store them in a hash table, or something like that. Each time you want to match, you can check against it if the given password has a match. The matching might be fast, but the cost of searching it on the disk or over the network on a remote server would make it slow. Don’t forget that you would need to do it for every password given by every user. How can we reduce the cost?
Well, a Bloom filter can help us here. How? I’m going to answer that, right after explaining how a bloom filter works. OK?
By definition, a Bloom filter can check if a value is possibly in the set or definitely not in the set. The subtle difference between possibly and definitely not is crucial here. This possibly in the set result is exactly why a Bloom filter is called probabilistic.
Using smart words, probabilistic means that a false positive is possible. In other words, there can be cases where the filter falsely thinks that the element is positive. But, a false negative is impossible.
Don’t be impatient. I’ll explain what it actually means shortly.
The bloom filter essentially consists of a bit-vector or bit-list(a list containing only either 0 or 1-bit value) of length m. Initially all values are set to zero, as shown below.

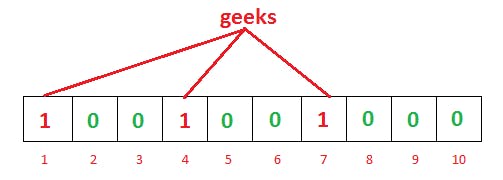
To add an item to the bloom filter, we feed it to k different hash functions and set the bits to one at the resulting positions. As you can see, in hash tables we would’ve used a single hash function, and, as a result, had only a single index as output. But in the case of the bloom filter, we would use multiple hash functions, which would give us multiple indexes.
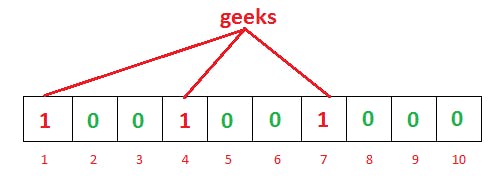
As you can see in the above example, for the given input geeks, our three hash functions will give three different outputs — one, four, and seven. We’ve marked them.
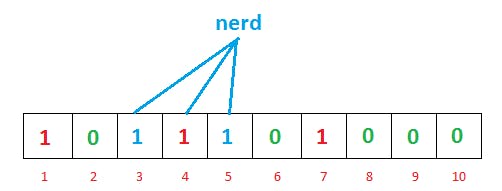
For another input, nerd, the hash functions give us three, four, and five. You might’ve noticed that index four is already marked by the previous geeks input. Hold that thought; this point is interesting, and we’re going to discuss it shortly.
We’ve already populated our bit vector with two inputs. Now we can check for a value for its existence. How can we do that?
Easy — just as we would’ve done it in a hash table. We would hash the searched input with our three hash functions and see what the resulting indexes hold.
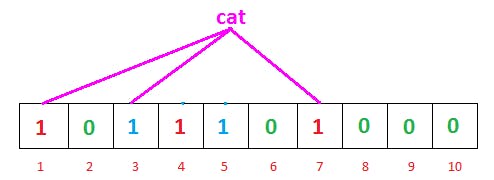
So, searching for cat, our hash functions are giving us one, three, and seven this time. And we can see that all of the indexes are already marked as one. That means we can say, “Maybe cat is already inserted on our list.”
But it isn’t. So, what’s went wrong?
Actually, nothing went wrong. The thing is, this is a case of a false positive. The Bloom filter is telling us that it seems that maybe cat was inserted before, because the indexes that should’ve been marked by cat are already marked (though by other different data).
So, if that’s the case, how is it helpful? Well, let’s consider if cat would’ve given us the output of one, six, and seven, instead of one, three, and seven. What would happen then? We can see that among three indexes, six is zero, which means it wasn’t marked by any of the previous inputs. That means, obviously, that cat was never inserted before. If it had been, there was no chance of six to be zero right? That’s how a bloom filter can tell for certain if a data is not on the list.
So, in a nutshell:
- If we search for a value and see any of the hashed indexes for this value is zero, then the value is definitely not on the list.
- If all of the hashed indexes are one, then maybe the searched value is on the list.
Is it starting to make sense? A little, maybe?
Fine, now, back to the password example we were discussing earlier. If we implement our weak password checking with this type of bloom filter, you can see that, initially, we would mark our bloom filter with our list of passwords. This will give us a bit vector with some indexes marked as one and others left as zero. As the size of the bloom filter will be fixed and not very large, it can easily be stored in the memory and also on the client side if necessary.
That’s why a bloom filter is very space-efficient. Where a hash table requires being of arbitrary size based on the input data, the bloom filters can work well with a fixed size.
So, every time a user enters their password, we will feed it to our hash functions and check it against our bit vector. If the password is strong enough, the bloom filter will show us that the password is certainly not in the weak password list and we don’t have to do any more query. But if the password seems weak and gives us a positive result ( which might be false), we will then send it to our server and check our actual list to confirm.
As you can see, most of the time we don’t even need to make a request to our server or read from the disk to check the list. This will be a significant improvement in speed of the application. In case we don’t want to store the bit-vector at the client side, we can still load it in the server memory and that will at least save some disk lookup time.
Also consider that if your bloom filters false positive rate is 1%(we will talk about the error rate in details later), that means among the costly round-trips to the server or the disk, only 1% of the query will be returned with false results. The other 99% won’t go in vain.
Not bad, huh?
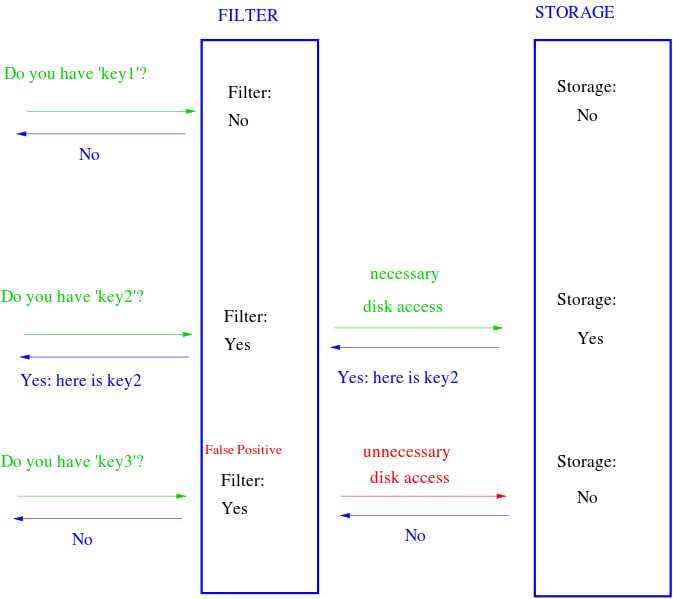
Bloom filter operations
The basic bloom filter supports two operations: test and add.
Test is used to check whether a given element is in the set or not.
Add simply adds an element to the set.
Now a little quiz for you.
Based on what we’ve discussed so far, is it possible to remove an item from the bloom filter? If yes, then how?
Take a two minute break and think about the solution.
Got anything? Nothing? Let me help you a bit. Let’s bring back the bit-vector after inserting geeks and nerd in it.
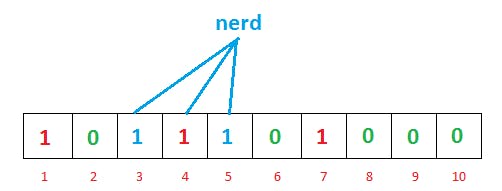
Now we want to remove geeks from it. So, if we remove one, four, and seven from the bit vector and convert them to zero, what will happen? You can easily see that next time, if we search for nerd as the index, four will show zero; it will tell us that nerd is not on the list, though it actually is. That means removal is impossible without introducing false negatives.
So, what’s the solution?
The solution is we can’t support a remove operation in this simple bloom filter. But, if we really need to have a removal functionality, we can use a variation of the bloom filter known as a counting bloom filter.
The idea is simple. Instead of storing a single bit of values, we will store an integer value, and our bit vector will then be an integer vector. This will increase the size, and it costs more space to give us the removal functionality. Instead of just marking a bit value to one when inserting a value, we will increment the integer value by one. To check if an element exists, check if the corresponding indexes after hashing the element are greater than zero.
If you are having a hard time understanding how a Counting bloom filter can give us a remove feature, I suggest you take a pen and paper and simulate our bloom filter as a counting filter, and then try a removal on it. Hopefully, you’ll get it easily. If you failed, try again. If you failed again, then please leave a comment and I’ll try to describe it.
Bloom filter size and number of hash functions
You might already understand that if the size of the bloom filter is too small, soon enough all of the bit fields will turn into one. Then, our bloom filter will return ‘false positive’ for every input. So, the size of the bloom filter is a very important decision to be made.
A larger filter will have less false positives, while a smaller one will have more. We can tune our bloom filter as precise we need it to be based on the false positive error rate.
Another important parameter is how many hash functions we will use. The more hash functions we use, the slower the bloom filter will be, and the quicker it will fill up. If we have too few, however, we may suffer too many false positives.
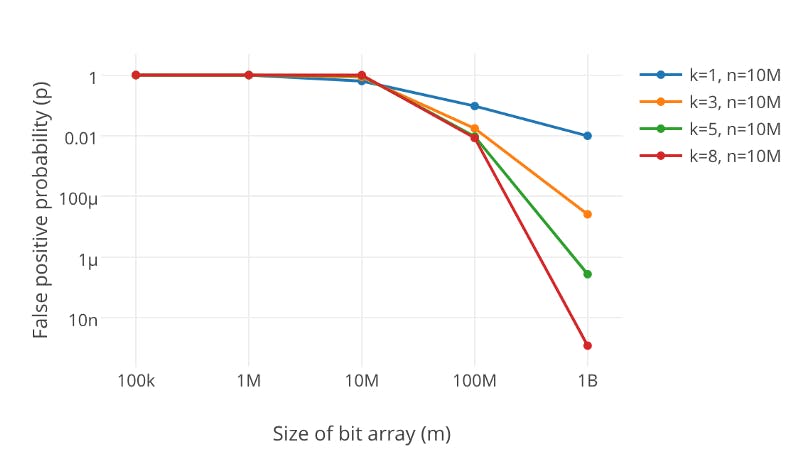
You can see from the above graph that increasing the number of hash functions, k, will drastically reduce the error rate, p.
We can calculate the false positive error rate, p, based on the size of the filter, m, the number of hash functions, k, and the number of elements inserted, n, with the formula:
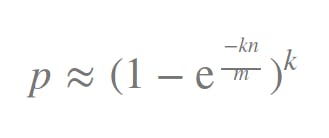
Don’t worry, we mostly need to decide what our m and k will be. So, if we set an error tolerance value, p, and the number of elements, n, by ourselves we can use the following formulas to calculate these parameters:
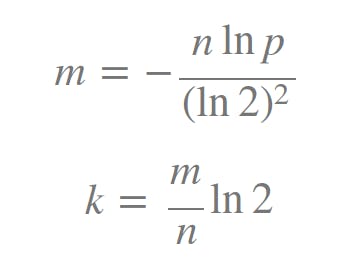
Another important point I also need to mention here. As the sole purpose of using bloom filter is to search faster, we can’t use slow hash functions, right? Cryptographic hash functions, such as Sha-1and MD5, won’t be good choices for bloom filters as they are a bit slow. So, the better choices from the faster hash function implementations would be murmur, the fnv series of hashes, Jenkins hashes, and HashMix.
Applications
Bloom filter is all about testing membership in a set. The classic example of using bloom filters is to reduce expensive disk (or network) lookups for non-existent keys. As we can see that bloom filters can search for a key in O(k) constant time, where k is the number of hash functions, it will be very fast to test non-existence of a key.
If the element is not in the bloom filter, then we know for sure we don’t need to perform the expensive lookup. On the other hand, if it is in the bloom filter, we perform the lookup, and we can expect it to fail some proportion of the time (the false positive rate).
For some more concrete examples:
- You’ve seen in our given example that we could’ve used it to warn the user for weak passwords.
- You can use a bloom filter to prevent your users from accessing malicious sites.
- Instead of making a query to an SQL database to check if a user with a certain email exists, you could first use a bloom filter for an inexpensive lookup check. If the email doesn’t exist, great! If it does exist, you might have to make an extra query to the database. You can do the same to search for if a username is already taken.
- You can keep a bloom filter based on the IP address of the visitors to your website to check if a user to your website is a returning user or a new user. Some false positive values for returning user won’t hurt you, right?
- You can also make a spell-checker by using a bloom filter to track the dictionary words.
- Want to know how Medium used bloom filters to decide if a user already read a piece? Read this mind-blowing, freaking awesome piece about it.
Do you still think that you won’t ever need bloom filter? Well, we don’t use all of the algorithms we’ve learned in our everyday life. But maybe someday it might save your arse. Who knows? Learning a new thing never hurts, right?
Originally published at: betterprogramming.pub/probabilistic-data-st..
